
🧮 Question 1: Aunt Lisa & Her Niece
“Aunt Lisa is 51 years old and her niece is 15 years old.
How old was Aunt Lisa when she was 4 times as old as her niece?”
🖼️ Step 0: Draw a model to understand the problem
👇 In the past, when Aunt Lisa was 4 times as old as her niece:
💙 Aunt Lisa = 4 units
💚 Niece = 1 unit
❤️ Difference = 3 units
✏️ Step 1: Find the current age difference
Aunt Lisa is 51 years old
Her niece is 15 years old
So, the difference is:
👉 51 − 15 = 36 years
🧠 This age difference stays the same — in the past, now, and in the future.
✏️ Step 2: Use the model to understand their ages in the past
From the picture:
Aunt Lisa = 4 units
Niece = 1 unit
So, the difference = 4 − 1 = 3 units
✏️ Step 3: Find how much each unit is worth
We know 3 units = 36 years
👉 So, 1 unit = 36 ÷ 3 = 12 years
✏️ Step 4: How old was Aunt Lisa then?
Aunt Lisa = 4 units
👉 4 × 12 = 48 years old
✅ Final Answer:
Aunt Lisa was 48 years old when she was 4 times as old as her niece.
🧮 Question 2A: Mike & Dan (Now)
“Mike is 7 times as old as Dan now.
In 8 years, their total age will be 64.
What is the age difference between Mike and Dan now?”
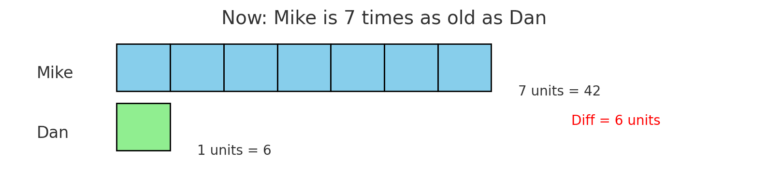
🖼️ Step 0: Let’s draw a model to understand the situation
In the model above:
💙 Mike = 7 units
💚 Dan = 1 unit
❤️ Difference = 6 units
✏️ Step 1: Find their total age now
We know their total age in 8 years = 64
Subtract 8 from Mike and 8 from Dan
👉 64 − 8 − 8 = 48 years
That means their total age now is 48.
✏️ Step 2: Use the model
Mike = 7 units
Dan = 1 unit
Total = 8 units
🧠 So, 1 unit = 48 ÷ 8 = 6 years
✏️ Step 3: Find their age difference
Difference = 6 units
👉 6 × 6 = 36 years
✅ Final Answer:
The age difference between Mike and Dan is 36 years
🧮 Question 2B: Mike & Dan (Future)
“How old will Dan be when Mike is 3 times as old as him?”
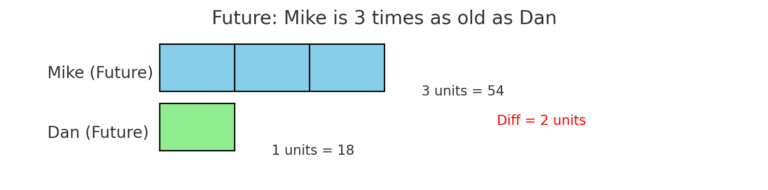
🖼️ Step 0: Look at the model above
In the future:
💙 Mike = 3 units
💚 Dan = 1 unit
❤️ Difference = 2 units
✏️ Step 1: Use the age difference from earlier
From Part A, we know:
➡️ Mike and Dan’s age difference = 36 years
(This stays the same over time!)
✏️ Step 2: Use the model
Difference = 2 units
👉 2 units = 36
🧠 So, 1 unit = 36 ÷ 2 = 18 years
✏️ Step 3: Dan’s future age
Dan = 1 unit
👉 1 × 18 = 18 years
✅ Final Answer:
Dan will be 18 years old when Mike is 3 times his age.
Now let’s move on to Question 3 — about balloons and ribbons at a party!
🎈 Question 3A: Balloons & Ribbons (Before)
“There were 5 times as many balloons as ribbons at first.
Mrs. Chan bought the same number of balloons and ribbons.
Now, there are twice as many balloons as ribbons.
If she has 24 balloons now, how many balloons did she buy?”
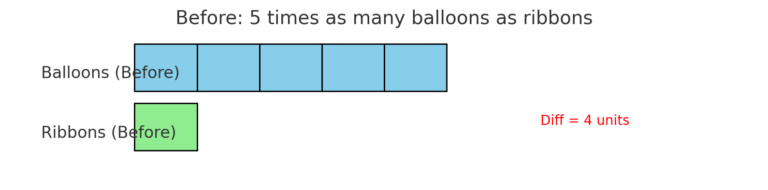
🖼️ Step 0: Model the situation before buying
From the model above:
🎈 Balloons = 5 units
🎀 Ribbons = 1 unit
❤️ Difference = 4 units
✏️ Step 1: After buying, the difference stays the same
Since Mrs. Chan bought the same number of balloons and ribbons,
👉 the difference between them remains 4 units
Now let’s draw the new situation — after buying.
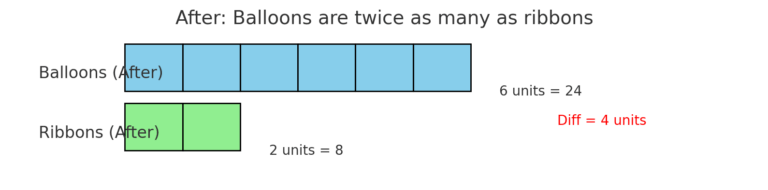
🎈 Question 3B: Balloons & Ribbons (After)
🖼️ Step 2: Model the situation after buying
In the model above:
🎈 Balloons = 6 units
🎀 Ribbons = 2 units
❤️ Difference = 4 units (still unchanged)
✏️ Step 3: Use the given info
Mrs. Chan now has 24 balloons
👉 6 units = 24
🧠 So, 1 unit = 24 ÷ 6 = 4
✏️ Step 4: How many balloons did she buy?
Originally:
Balloons = 5 units
Now:
Balloons = 6 units
So she bought 1 extra unit of balloons
👉 1 × 4 = 4 balloons
✅ Final Answer:
Mrs. Chan bought 4 balloons

